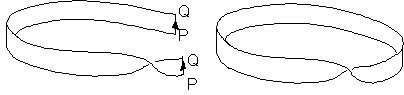Möbius Şeridinin İncelenmesi
Bir yüzeyi neresinden tutmalı
 Yüzeyleri en
basit anlamda incelemek için yüzeyi, verilen bir koordinat
sistemi için belirli şartlardaki bir denklemi sağlayan
noktalar kümesi olarak alabiliriz. İncelemede kolaylık
sağlaması açısından bazı aynı özellikleri gösteren
yüzeyleri aynı sınıflara koyarak bir sınıflandırmaya
gidelim. Bu sayede Möbius şeridinin Öklid uzayındaki özel
bir gösterilimi ile kısıtlı kalmayacağız, etrafımızdaki
Möbius şeritlerini de görmeyi başaracağız. Şimdi
yüzeylerin bazı ortak özelliklerini nasıl öne
çıkarabileceğimizi inceleyelim.
Yüzeyleri en
basit anlamda incelemek için yüzeyi, verilen bir koordinat
sistemi için belirli şartlardaki bir denklemi sağlayan
noktalar kümesi olarak alabiliriz. İncelemede kolaylık
sağlaması açısından bazı aynı özellikleri gösteren
yüzeyleri aynı sınıflara koyarak bir sınıflandırmaya
gidelim. Bu sayede Möbius şeridinin Öklid uzayındaki özel
bir gösterilimi ile kısıtlı kalmayacağız, etrafımızdaki
Möbius şeritlerini de görmeyi başaracağız. Şimdi
yüzeylerin bazı ortak özelliklerini nasıl öne
çıkarabileceğimizi inceleyelim.
Mesela üç boyutlu Öklid uzayı içindeki z =
xy (1) ve 2Z = X2 - Y2 (2)
denkemlerinin belirttikleri yüzeyleri ele alalım. Biraz dikkat
edilirse, her iki yüzey de benzer bazı özellikler gösterir.
Hatta (1) yüzeyinin denkleminde x = (X+Y) / 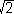 ve y =
(X-Y) /
ve y =
(X-Y) / 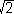 alalım. O zaman z = xy = (X+Y) (X-Y) / 2 = (X2 - Y2)
/ 2, her iki tarafı 2 ile çarparsak (2) denkleminin elde
edildiği görülür, yapılan iş ise sadece bir katı cisim
hareketi, yani bir afin dönüşümdür, bu yüzeyler koordinat
sistemi seçimi dışında aynıdır. O halde aynı tür
yüzeyleri gruplarken, yüzey gruplarının seçilen koordinat
sisteminden bağımsız olmasını isteyeceğiz. Bunun için de
ölçümlere bağımlı kavramlar kullanmak yerine daha genel
kavramlar kullanmalıyız. Burada ise işin içine topoloji
girer.
alalım. O zaman z = xy = (X+Y) (X-Y) / 2 = (X2 - Y2)
/ 2, her iki tarafı 2 ile çarparsak (2) denkleminin elde
edildiği görülür, yapılan iş ise sadece bir katı cisim
hareketi, yani bir afin dönüşümdür, bu yüzeyler koordinat
sistemi seçimi dışında aynıdır. O halde aynı tür
yüzeyleri gruplarken, yüzey gruplarının seçilen koordinat
sisteminden bağımsız olmasını isteyeceğiz. Bunun için de
ölçümlere bağımlı kavramlar kullanmak yerine daha genel
kavramlar kullanmalıyız. Burada ise işin içine topoloji
girer.
Topoloji, matematiğin bir dalı olarak XIX. yüzyılın
sonlarında ünlü Fransız matematikçi Henri Poincaré'nin
çalışmaları ile sistematik oluşumuna başlamaıştır.
Aslında, topoloji alanındaki araştırmaların başlangıcı G.
Riemann'ın XIX. yy. ortalarına rastlayan fonksiyonlar teorisi
ile ilgili çalışmaları olarak alınabilir. Fakat ilk
topolojik kavramları ortaya atıp üzerine derin bir teoriyi
kuran Poincaré'dir. Bakın Poincaré topolojiyi (o zamanlar analysis
situs deniyordu) nasıl tanımlamış:
- Analysis situs, geometrik şekillerin, sadece
alışılmış uzayda değil, üçten fazla boyutlu
uzaylarda da niteliklerini öğrenmemizi sağlayan bir
bilimdir. Üç boyutlu uzayda analysis situs, bizim için
neredeyse sezgisel bir bilgidir. Üçten fazla boyutlu
uzaylarda ise, analysis situs karşmıza çok büyük
zorluklar çıkarır, üstesinden gelmeye çalışmak
için ise, bireyin bu bilimin büyük önemine inanmış
olması gerekir. Eğer bu önem herkes tarafından
anlaşılmamış ise, demek ki herkes yeterince üzerine
düşünmemiştir.
Bir geometrik şeklin niteliksel özelliklerini daha iyi
anlamak için bir küreyi, elastik bir balon olarak düşünelim.
Bu küreyi, parçalamadan veya farklı iki noktasını
yapıştırmadan şeklinde meydana getirilebilen tüm
değişimlere homeomorfizma denir (yani birebir, örten,
kendi ve tersi sürekli bir fonksiyon), ve bir şeklin böyle bir
dönüşüm altındaki görüntüsü ile bir homeomorfik taklidi
elde edilir. O halde, kürenin niteliksel özellikleri, tüm
homeomorfik taklitleri ile paylaştığı özellikleridir. Bu
özelliklere de topolojik özellikler denir.
Möbius şeridi
Artık bir Möbius şeridinin tanımını verebiliriz.
Geometrik olarak, uzunca bir şeridin bir ucunu 180 derece
büküp diğer ucu ile birleştirirsek elde edilen şeride Möbius
şeridi denir (Bakınız şekil 1). İlk olarak 1861'de Johann
Benedict Listing tarafından tanımlanmıştır, dört yıl
sonra ise Möbius yayınladığı bir çalışmasında
tanımını vermiş, şeridin tek yüzlü olduğunu,
yönlendirilememesi ile açıklamıştır, bunun için de
yüzeyin yönlü üçgenler ile kaplı olduğunu varsaymış,
fakat tüm yüzeyin aralarında uyumlu yönlü üçgenler ile
kaplanamayacağını göstermiştir.

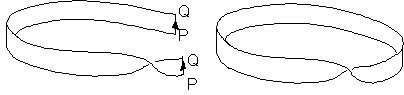
Şekil 1. Möbius şeridinin elde edilişi.
Şimdi biraz daha farklı ve kullanışlı bir gösterilim
geliştirip Möbius şeridini incelemeye başlayalım:
Şekil 2(a)'daki gibi, bir kareyi aldığımızda, aynı
isimlendirilen kenarlar oklar yönünde birleştiriliyor
anlamına gelsin. O halde ABCD diye bu kareyi adlandırıp bir
koordinat sistemi üzerine yerleştirebiliriz. A(0,0) ve C(1,1)
olsun (Yani, bu örnekte, AD ile BC ters yönde
birleştiriliyorlar).
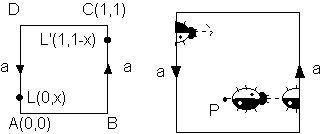
Şekil 2(a). Möbius şeridinin temel çokgeni, (b) Böceğin
hareketi.
Şekilde de görülebileceği gibi AD üzeindeki L(0,x) ve BC
üzerindeki L'(1,1-x) noktaları yapıştırma sonucunda aynı
noktalar olacaktır. Bu Möbius şeridi üzerinde, P noktasından
gezmeye başlayan bir böceğin kısa gezintisini Şekil 2(b)'de
görebiliriz. BC sınırına gelen böcek, BC AB ile
yapıştırıldığından karşılık gelen yerden duraksamadan,
hiçbir değişiklik hissetmeden gezinmeye devam eder. Böceğin
BC'yi geçince simetrisini görünce çok da şaşırmamak
gerekli. Zaten Möbius'un, bu şeridin yönlendirilemez olduğunu
demesi bundan ibarettir, böcek AD be BC'nin orta noktalarını
birleştiren doğru üzerinde gezseydi, başlangıç konumuna
tekrar vardığında sınırları aşmamasına rağmen, önceden
sırtı bize yönelmişken, bu sefer karnı bize yönelmiş olur
(simetrisini gördüğümüzden). Böceğin hareketini, bir boya
fırçasının hareketi olarak düşünsek, şeridin bir
yüzünü boyamaya başlayan bir fırça, sınırdan öteki yüze
atlamadan, her iki yüzü boyardı, yani aslında yüz sayısı
iki değildir. Böceği düşenmeye devam edelim. Bu böcek bir
küre yüzeyi üzerinde gezseydi böyle bir durumla asla
karşılaşamayacaktı. Fakat dünyamız bir Klein şişesi
olsaydı bu durumla karşılaşma ihtimali olurdu. Öncelikle
Klein şişesinin ne olduğunu hatırlayalım:
Möbius şeridi gibi tek yüzlü olan Klein şişesi, kapalı
bir yüzeydir. Bir silindirin sınır çemberlerini farklı
yönlerde birleştirirsek elde edeceğimiz şekil bir Klein
şişesidir. Bu tanıma göre Klein şişesinin temel çokgenini
şekil 3(a)'daki gibi çizeriz, elde ettiğimiz yüzeyin bir
çizimi ise şekil 3(d)'de görülüyor. Kenarların
birleştirilmelerini biraz daha açık yazmak istersek, AD
üzerindeki (0,x) noktası BC üzerindeki aynı hizalı (1,x)
noktasıyla, AB üzerindeki (x,0) noktası ise DC üzerindeki
(1-x,1) noktası ile birleşir. Maalesef üç boyutlu Öklid
uzayında bu şişeyi gösterebilmek için silindirin kendi
kendisini kesmesi gerekmektedir. Aslında yüzey üzerindeki
kesişimi, bir hayaletin bir duvardan öteye geçmesi gibi
düşünelim.
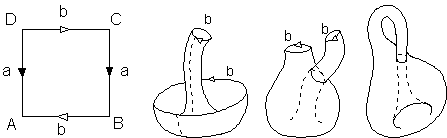
Şekil 3(a) Klein şişesinin temel çokgeni ve (b)-(d)
kenarların yapıştırılması.
Bu şişenin tek yüzlü olması, yaklaştığınızda Möbius
şeridi kokuları almanıza yol açar, hatta, şimdi size büyük
bir iddiamız var: Klein şişesi, Möbius şeridi içerir. Bunu
ise Klein şişesini basit kapalı bir eğri ile keserek
göstereceğiz. Şekil 4(a)'de görülen kesik çizgiler boyunca
Klein şişesinin temel çokgenini keselim, sonra da kurallara
uygun şekilde birleştirmeyi deniyelim:
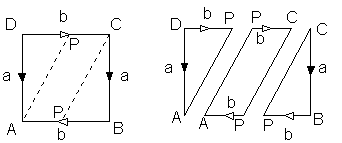
Şekil 4(a) Nasıl kesmeli, (b) kesince, (c) tekar düzenlenince
İşlemleri Klein şişesinin temel çokgeni ABCD üzerinde
yapalım. Şekil 4(a)'da görülen APC eğrisi Klein şişesi
üzerinde basit kapalı bir eğridir (dikkat edilmeli ki çokgen
üzerinde iki eğri var gibi gözükse bile nasıl farklı
görünen iki noktanın adı P ise, eğri de bir P noktasına
varınca, diğerinden devam eder). Şekil 4(b)'de çokgenin
kesilmiş halini görüyoruz. Burada APCP dörtgeninin oklar
yönünde birleştirilince bir Möbius şeridi olduğunu
görünce koku duyumuzda yanılmadığımızı görürüz. Peki
geri kalan parçalar nedir? AD ile BC doğruları ok yönünde
birleştirilince, Şekil 4(c)'de görüldüğü üzere, bir tane
daha Möbius şeridi elde ettiğimizi farkederiz! O halde her
Klein şişesi, bünyesinde iki Möbius şeridi içerir, daha
güzel söylemek gerekirse, iki Möbius şeridi alıp
sınırları boyunca birbirine yapıştırırsak, elde
edeceğimiz Klein şişesinden başka birşey değildir.
Şimdi ise son olarak Möbius şeridinin kendisini kesmeyi
deniyelim. Acaba Möbius şeridini boylu boyunca kesersek ne elde
edeceğiz? Mesela sınırından genişliğinin dörtte biri
uzaklıktan kesmeye başlayalım. Bunu Möbius şeridinin temel
çokgeni üzerinde göstermek istersek Şekil 5'deki manzara
karşımıza çıkar.
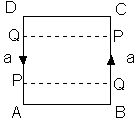
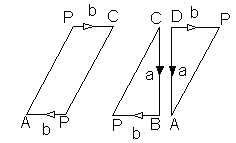
Şekil 5. Möbius şeridini kesince ne elde ederiz?
PQP basit kapalı bir eğridir, kesildikten sonra AD
kenarının üzerindeki PQ parçası, BC üzerinde karşılık
gelen QP parçası ile ters yönde birleştirilir, yani bir
Möbius şeridi elde edilir, hem de annesinin yarı genişliğine
sahip bir şerit. APQB ile PCDQ birleştirildiğinde ise başka
bir şerit daha elde ederiz. Bu şerit ise BQ ile QD ters yönde,
sonra da PC ile AP de ters yönde birleştirileceğinden tam bir
dönme içeren bir şerit elde edilir, doğal olarak artık bu
ükü yüze sahiptir, topolojik olarak bir silindirdir, ayrıca
kolayca gösterilebileceği gibi silindir ise topolojik olarak
bir noktası eksik düzlem ile aynıdır.
Bu yazıyı ufak bir soru ile noktalıyoruz. Möbius şeridini
tam ortası boyunca kesseydik ne olurdu? Bunu bir limit olarak
düşünün, yani PQ eğrilerini yavaş yavaş merkez doğrusuna
yaklaştırın. Hepinize eğlenceli ve topolojili günler
dileğiyle.
MATEMATIK SAYFASINA
GERI DONUS
KLEIN SISESINE GERI
DONUS
 Yüzeyleri en
basit anlamda incelemek için yüzeyi, verilen bir koordinat
sistemi için belirli şartlardaki bir denklemi sağlayan
noktalar kümesi olarak alabiliriz. İncelemede kolaylık
sağlaması açısından bazı aynı özellikleri gösteren
yüzeyleri aynı sınıflara koyarak bir sınıflandırmaya
gidelim. Bu sayede Möbius şeridinin Öklid uzayındaki özel
bir gösterilimi ile kısıtlı kalmayacağız, etrafımızdaki
Möbius şeritlerini de görmeyi başaracağız. Şimdi
yüzeylerin bazı ortak özelliklerini nasıl öne
çıkarabileceğimizi inceleyelim.
Yüzeyleri en
basit anlamda incelemek için yüzeyi, verilen bir koordinat
sistemi için belirli şartlardaki bir denklemi sağlayan
noktalar kümesi olarak alabiliriz. İncelemede kolaylık
sağlaması açısından bazı aynı özellikleri gösteren
yüzeyleri aynı sınıflara koyarak bir sınıflandırmaya
gidelim. Bu sayede Möbius şeridinin Öklid uzayındaki özel
bir gösterilimi ile kısıtlı kalmayacağız, etrafımızdaki
Möbius şeritlerini de görmeyi başaracağız. Şimdi
yüzeylerin bazı ortak özelliklerini nasıl öne
çıkarabileceğimizi inceleyelim.