Felix Klein'ın isim babalığı yaptığı bir ilginç
yüzeyle tanışmak üzeresiniz. Klein şişesinin ilginç
özelliklerinden biri bir yüzey (dolayısıyla iki boyutlu)
olmasına rağmen bulunduğumuz üç boyutlu uzayda bir makedi
yapılamaz olması. Bu nedenle resmini de çizemeyiz! Fakat sizin
insafınıza sığınarak aşağıdaki şekli sunalım:
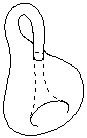 Daha ayrintili bir klein
şişesi resmi için TIKLATIN. Resimde
ucu tekrar içine bükülen ve zeminiyle birleşen bir şişe
görülüyor. Klein şişesi ise bir manifold olduğundan (yani
üzerinde yürüyen görüşü kısıtlı bir böceğin düzlem
sanacağı uzaylar) kendi kendini kesmemelidir, bu nedenle dört
boyutlu uzayda gerçek bir Klein şişesi oluşturulabilir:
nasıl düzlemde kesişen iki doğru varsa biri üçüncü
boyutta ötelenerek kesişimden kurtulabilirsek, bu durumda da
kesişim bölgesindeki noktaların bir komşuluğu dördüncü
boyutta uzaklaştırılır.
Daha ayrintili bir klein
şişesi resmi için TIKLATIN. Resimde
ucu tekrar içine bükülen ve zeminiyle birleşen bir şişe
görülüyor. Klein şişesi ise bir manifold olduğundan (yani
üzerinde yürüyen görüşü kısıtlı bir böceğin düzlem
sanacağı uzaylar) kendi kendini kesmemelidir, bu nedenle dört
boyutlu uzayda gerçek bir Klein şişesi oluşturulabilir:
nasıl düzlemde kesişen iki doğru varsa biri üçüncü
boyutta ötelenerek kesişimden kurtulabilirsek, bu durumda da
kesişim bölgesindeki noktaların bir komşuluğu dördüncü
boyutta uzaklaştırılır.
En kolayı yüzeyi şekildeki gibi düşünüp yüzey
üzerinde yürüyen bir böcek kesişim bölgesine vardığında
kesişimi görmeden (bir hayalet gibi) yürüyüşünde bir
değişim olmadan geçsin. Bu düşünce tarzı ile Klein
şişesinin tek yüzlü olduğu rahatça söylenir: bir
yüzünden boyamaya başladığımızda öteki yüze geçmeden
(!) boyamaya çalışırsak boyanmamış yerin kalmadığı
görülür, bu ise Klein şişesinin bir Möbius
şeridi içermesinden kaynaklanır.
İnsan ister istemez 'bu yüzey de nereden çıktı'
diye düşünüyor. Bazıları ise 'Klein şişesini nasıl
kesmeli ki iki Möbius şeridi elde edeyim' diyor.
Gerçekten, Scientific American dergisinin Mart 1998 sayısında
bir cam ustasının yarattığı Klein şişeleri ve varyanları
görülmeye değer. Bunları yapan Alan Benett amacının
Klein şişesini uygun bir eğri boyunca kesip üç kez burulmuş
iki Möbius şeridi elde etmek olduğunu söylemiştir. Genelde
bu topologlar için önemli değildir çünkü yüzeyler ve
manifoldlar içinde bulundukları uzaydan bağımsız olarak
vardır; başka bir uzayın içine gömülme şekilleri farklı
bir problemdir. Sonuç olarak insanı düşündüren ve
eğlendiren, ayrıca topologlara güzel örnek ve ters örnekler
yaratan bir yüzeydir. Scientific American'daki makale bir
soruyla bitiyor: Klein şişesi üzerinde öyle bir eğri bulun
ki bu eğri boyunca kestiğinizde elinizde bir ve yalnız bir
tane Möbius şeridi kalsın. Bulabildiniz mi?
Klein şişesini algılamayı kolaylaştıran başka yorumlar
da var. "Möbius seridinin incelenmesi" yazısında
anlatılan ve topologların çok sevdiği bu tanımı
hatırlatalım:
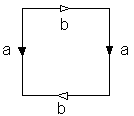 Bir kare alıp
yandaki şekilde belirtilen gibi karşılıklı kenarlarını
oklar yönünde yapıştıralım. Bu takdirde elde edeceğimiz
Klein şişesidir! Bu işleme topolojide bir uzayın bölüm
uzayını oluşturma denir, uzayın bazı noktalarını aynı
kabul etmek demektir. Yüksek boyutlu uzaylarda düşünmek
yerine düzlemsel bir şekil olan bu kare üzerinde düşünelim,
Bir kare alıp
yandaki şekilde belirtilen gibi karşılıklı kenarlarını
oklar yönünde yapıştıralım. Bu takdirde elde edeceğimiz
Klein şişesidir! Bu işleme topolojide bir uzayın bölüm
uzayını oluşturma denir, uzayın bazı noktalarını aynı
kabul etmek demektir. Yüksek boyutlu uzaylarda düşünmek
yerine düzlemsel bir şekil olan bu kare üzerinde düşünelim,
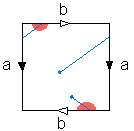 o haldeKlein
şişesi üzerindeki bir noktanın komşuluğu şekildeki
kırmızı daire olarak ifade edilebilir, Klein şişesi
üzerindeki bir yol ise bu kare içinde, sınırların
yapıştırıldığı göz önünde bulundurularak, şekilde
örneklenmiştir.
o haldeKlein
şişesi üzerindeki bir noktanın komşuluğu şekildeki
kırmızı daire olarak ifade edilebilir, Klein şişesi
üzerindeki bir yol ise bu kare içinde, sınırların
yapıştırıldığı göz önünde bulundurularak, şekilde
örneklenmiştir.
Bu gösterilimin geliştirilmesi ile, Klein şişesini kesmek
de daha da kolaylaştı! Örneğin bir köşegen boyunca kesersek
ne elde ederiz?
Bu sayfadaki resimler MAT resim galerisinden
alınmıştır. KAYNAK: Ege üniversitesi
matematik arastirma toplulugu web sayfasi
MATEMATIK SAYFASINA
GERI DONUS
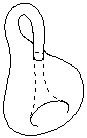 Daha ayrintili bir klein
şişesi resmi için TIKLATIN. Resimde
ucu tekrar içine bükülen ve zeminiyle birleşen bir şişe
görülüyor. Klein şişesi ise bir manifold olduğundan (yani
üzerinde yürüyen görüşü kısıtlı bir böceğin düzlem
sanacağı uzaylar) kendi kendini kesmemelidir, bu nedenle dört
boyutlu uzayda gerçek bir Klein şişesi oluşturulabilir:
nasıl düzlemde kesişen iki doğru varsa biri üçüncü
boyutta ötelenerek kesişimden kurtulabilirsek, bu durumda da
kesişim bölgesindeki noktaların bir komşuluğu dördüncü
boyutta uzaklaştırılır.
Daha ayrintili bir klein
şişesi resmi için TIKLATIN. Resimde
ucu tekrar içine bükülen ve zeminiyle birleşen bir şişe
görülüyor. Klein şişesi ise bir manifold olduğundan (yani
üzerinde yürüyen görüşü kısıtlı bir böceğin düzlem
sanacağı uzaylar) kendi kendini kesmemelidir, bu nedenle dört
boyutlu uzayda gerçek bir Klein şişesi oluşturulabilir:
nasıl düzlemde kesişen iki doğru varsa biri üçüncü
boyutta ötelenerek kesişimden kurtulabilirsek, bu durumda da
kesişim bölgesindeki noktaların bir komşuluğu dördüncü
boyutta uzaklaştırılır.  Bir kare alıp
yandaki şekilde belirtilen gibi karşılıklı kenarlarını
oklar yönünde yapıştıralım. Bu takdirde elde edeceğimiz
Klein şişesidir! Bu işleme topolojide bir uzayın bölüm
uzayını oluşturma denir, uzayın bazı noktalarını aynı
kabul etmek demektir. Yüksek boyutlu uzaylarda düşünmek
yerine düzlemsel bir şekil olan bu kare üzerinde düşünelim,
Bir kare alıp
yandaki şekilde belirtilen gibi karşılıklı kenarlarını
oklar yönünde yapıştıralım. Bu takdirde elde edeceğimiz
Klein şişesidir! Bu işleme topolojide bir uzayın bölüm
uzayını oluşturma denir, uzayın bazı noktalarını aynı
kabul etmek demektir. Yüksek boyutlu uzaylarda düşünmek
yerine düzlemsel bir şekil olan bu kare üzerinde düşünelim,
 o haldeKlein
şişesi üzerindeki bir noktanın komşuluğu şekildeki
kırmızı daire olarak ifade edilebilir, Klein şişesi
üzerindeki bir yol ise bu kare içinde, sınırların
yapıştırıldığı göz önünde bulundurularak, şekilde
örneklenmiştir.
o haldeKlein
şişesi üzerindeki bir noktanın komşuluğu şekildeki
kırmızı daire olarak ifade edilebilir, Klein şişesi
üzerindeki bir yol ise bu kare içinde, sınırların
yapıştırıldığı göz önünde bulundurularak, şekilde
örneklenmiştir.